| <- Funktionsweise am Röhrenverstärker |
LowLevel-URI
A profound knowledge about how electrical voltage, current and resistors are connected is in the foundation of understanding any electrical circuit:
ChapterOne.
![]()
Voltage

A large lake is located on a mountain. The mountain shall be the minus pole and the valley be plus.
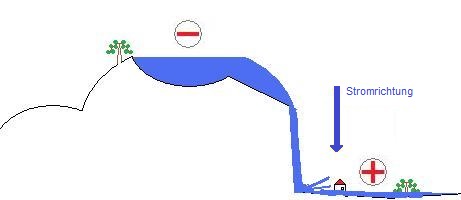
If the hillslope is suddenly blasted off, the water falls down massively. There is almost no resistance in the free fall. A considerable current is flowing, similar to short circuit.

The bigger the difference between peak and valley, the more powerful the effect of every falling drop and so the whole water mass. The released power in 'splashing water' at the arrival at the valley is determined by the amount of water as well as the falling height. The height difference, which exists even if there is no water flowing down as long the lake still has water, is, in the water model, equivalent to the voltage (U). The higher the mountain, the higher the present voltage.

For ecological reasons it is understandable that the mountain-blast-short-circuit-scenario should be avoided.A pipe would be better, laid from the lake down to the valley to get water or energy there. With a water column inside and a steady water load that takes effect over the distance from peak to valley,the pipe brings the desired features of the model:
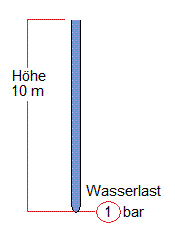
A top opened pipe with the height of 10 meters (it does not matter what diameter) filled with water will have a preasure of 1 bar at the bottom. You can hold 1 bar preasure with your thumb.
The filled up pipe at the supposed 100 meter mountain lake generates a powerful 10 bar water load at the valley. That would be twice the usual domestic water pressure (that is in germany) and holding this pressure by hand is impossible.

This pressure from the present water load in the pipe determines the level of the voltage in this model. For example 5 bar (from 50 meters heigth) could stand for 5 Volts of voltage or 1 bar for 1 Volt. (from 10 meters heigth)
 |
 |
 |
The 100 meter long mountain lake pipe is closed tight with a rubber cap down at the valley. If the hydrostatic head rises the rubber cap will bend further like a membrane. This way every value between 0 and 10 can be displayed without water draining. In principle this is similar to measuring voltage (U) in Volts (V).
![]()
![]()
electrical current

Unfortunately this misunderstanding has prevailed until today:
The electrical, technical direction if the current in a circuit leads from plus to minus. When this agreement was made, people did not know about electrons.
The electronical direction of the current on the contrary, leads from minus to plus. The water model takes the electrons into consideration - direction of current, meaning their way from negativ minus (pole) to positive (pole).
 |
 |
From the lake downwards the water mass stream through a giant pipe. How many liters per second pass through as a flow rate corresponds to the measure of the electrical current (I) in Ampere (A).
![]()
alternating current

The piston forces a constantly changing movement onto to water circulation. The drive is the circular motion of the crank wheel. A full rotation corresponds to a completed reciprocating motion in the water circuit. The frequency describes how many of these alternating cycles are completed per second. In the model the crank wheel rotation, that means the corresponding alternating wave, takes one second. So the frequency is 1, translated into the (SI unit): Hertz (1 Hz). It doesn't matter whether the oscillation is measured at the crank wheel or elsewhere in the alernating water current, everywhere is the same sinusoidal oscillation.
Electrical alternating current in europes plug sockets oscillates 50 times per second. (50 Hz) are to fast for an optical differentiation. You can hear this 50 Hz frequency allready, for example at transformators as a deep humming sound.
![]()
| The amount of theie energy of the water power is the result of the falling height multiplied by the volumetric current.
Splashing-Water-Power (P) = mountain height (in meters) multiplied by the amount of water (in liters per second) is comparable with: electrical power (P) = Voltage (in Volts) multiplied by the current (in Ampere) |
![]()
SecondChapter

Electrical Resistance

In the water example a resistor, like the "cocktail fruit in a straw" limits the maximal current.

Electrical resistors restrain the current likewise due to their limited conductibility.
The lost power of the electron current at the resistor changes mostly into heat.

Electrical resistors for example can be appliances like refrigerators, lamps and tv sets.

With the specialised component, the resistor, you can set different energy amounts of voltage and current in electronic circuits for a desired purpose, according to the resistors conductivity. The colors that are printed on a resistor mark the electric properties of that restor. Translating with classic "color chart" (externalLink) here shows a metal film resistor 6040 Ω with 1% tolerance.

The effectiveness of the influence is set in the value of the resistor. The higher the value, the bigger the limitation of the current.
The value of an electrial resistor (R) is specified in Ohm (Ω).

Ohm's law (the law of the resistor) R=U/I describes this inseparable dependency of the voltage U (in Volt), the value of the applied resistor R (in Ω Ohm)),and the possible current I (in Ampere) which can pass through the resistor.
![]() /
/
![]() =
= ![]()
So if at a present voltage (U) of 1 Volt (one bar, so 10 meters water heigth), exactly 1 Ampere (one litre of water per second) current (I) flows, then there is a resistor (R) in in the current flow which has value of 1 Ω Ohm. (Pipe section with a fitting cocktail fruit for the water flow of exactly 1 litre/second at 10 m water load)
At
a voltage of 2 Volts (20
meters water load)
the current rises proportionally to 2 Amperes (2
litres of water per second)
at the presence of the same 1 Ohm (Cocktail-)
resistor
and so forth.
![]()
|
R=U/I |
I=U/R |
U=R*I |
By changing the formula mathematically every other unknown value of the resistor-voltage-current-correlation can be calculated if two of the values are known.
![]()
Resistors can in their value be fix,
|
|
|
...but others can be alterable:


The shut-off slide at the muzzle represents all possible water resistors from closed to opened. For the water it is an alterable resistor.
![]()
In an amplifier circuit for example resitors rather bigger than 1 Ohm like zB. 4,7kΩ = 4.700 Ohm, or Megaohm: 1M = 1.000.000 Ohm would be needed. It make sense to limit the multiplicity of resistor values a controllable degree. In Europe resistors, as well as capacitors, are standardised as fixed values within the "E96- series" and partitioned in about 800 purchasable units. In Addition to that there are different sizes for different load tolerance (in Watt), potentiometer and trimmer as alterable resistors or special types like temperature sensors and photoconductive cells.

The power source itself is a resistor too. In a short-circuit situation its resistance sets the maximum current that can flow.
Furthermore strong currents require thicker wires or bigger pipes. If the diameter is too small, power will be lost due to congestion and jostle.
![]()
LastChapter
|
|
|
|
I.) Let there be two resistors built into to water way. Resistor R1 first limits the flow rate. Resistor R2 is non-effective at the moment and so practically absent. The rubber cap of the voltmeter clamps betweeen R1/R2 and shows no increase of the pressure. All the water coming from R1 can run unhampered through R2.
II.) Now R2, with the smaller passage stands against the current, here with a wider opened R1. Not all water from R1 can pass simultaneously through R2. The part of the water that can't pass will have to wait. The afflux leads to a rise of the pressure between the resistors.
R=U/I determines: A rising voltage, or pressure, preceding a resistor, leads to a rising of the current which flows to that resistor accordingly. This means: "what does not fit"-afflux"-pressure preceding R2 forces more and more water through R2, at the same time, and will stand at the same level if at last the same amount of water is pressed through R2 as the water coming on from R1. The cap-voltmeter, between both the resistors shows us this average afflux pressure- "voltage value".
III.) is the other extremum, according to I.) Would the water flow through R2 be closed, the maximum mountain-pressure at R1 on the cap-o-meter - so the maximum "voltage" at the measuring point between the two resistors.
***
Consequently every arbitrary voltage value can, in the bounds of extremum I. and III. be measured if only the fitting ratio of the values of the resistors R1 and R2 has been found...
... and it be assumed that the mountain-power-source delivers every demanded spray-nozzle-current, that means the overall current passing through both of the resistors at all times.
From this the following can be stated:
(page in German)
|
For now we will leave aside the discussion about how the current works when "resistors are connected in parallel. |
Sept,2012
(2009)